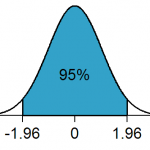
Statistische … was?
Wenn etwas statistisch signifikant ist, sagen wir, dass das Ergebnis einer Untersuchung (z.B. der Wirkung eines Medikamentes) nicht zufällig gewesen sein kann.
Die statistisch Signifikanz (der sog. p-Wert) gibt an wie unwahrscheinlich es ist, dass das Ergebnis einer Untersuchung zufällig passiert ist. Je kleiner er ist, desto unwahrscheinlicher, dass der Zufall am Werk war. Umgekehrt halten wir ein statistsiches signifikantes Untersuchungsergebnis für ein Ergebnis, dass nicht zufällig passiert ist.
Was?!
Schauen wir uns dazu ein einfaches Beispiel an.
Ein einfaches Beispiel: Kinder beim Zähneputzen.
Kinder sollen sich abends vor dem Schlafengehen die Zähne putzen. Bei mir war das so und bei den meisten Kindern, die ich kenne, ist das auch heute noch so. Und, es hat sich nicht viel geändert, seit ich klein war: Kinder haben noch immer nicht so große Lust dazu. Also muss man sie immer wieder daran erinnern. Sagen wir eine Mutter erinnert ihre Tochter Jule, sie soll sich die Zähne putzen. Jule entgegnet nun aber: “Ich habe mir schon die Zähne geputzt!” Allerdings ist ihre Zahnbürste noch trocken.
Unsere Schlussfolgerung ist: da die Zahnpürste noch trocken ist, ist es unwahrscheinlich, dass sich Jule schon die Zähne geputzt hat. Ihre Mutter wird also davon ausgehen, dass Jule die Zähne noch nicht geputzt hat und sie nochmals ins Bad schicken.
Aus Sicht des Statistikers sieht die Situation so aus:
- Daten: die Zahnbürste ist trocken
- Hypothese: Jule hat sich die Zähne schon geputzt
- Folgerung: falls die Hypothese wirklich wahr wäre, wären die Daten außergewöhnlich, daher verwerfen wir diese Hyothese und nehmen die stattdessen ihr Gegenteil (Jule hat ihre Zähne noch nicht geputzt) als wahr an
Wie bereits am Anfang gesagt: die statistische Signifikanz gibt an wie wahrscheinlich es ist, dass das Ergebnis einer Untersuchung zufällig ist.
Probleme bei statischen Tests
Interessant ist auch folgendes: nur, weil wir ein Test aussagt, dass eine Untersuchung statistische signifikant wahr, heißt das noch lange nicht, dass sie auch notwendigerweise wahr ist. Beispielsweise hätte Jule auch so vor dem Zähneputzen drücken können, indem sie die Zahnbürste einfach eine Sekunde unter laufendes Wasser hält. Dann ist sie nass und es erscheint so, als ob sie sich die Zähne geputzt hätte – zumindest, wenn wir die Trockenheit bzw. Nassheit der Zahnbürste als alleiniges Kritierum für die Untersuchung heranziehen. Um also sicher zu gehen müssten noch weitere Faktoren untersucht werden: z.B. Füllstand der Zahnpastatube oder die Menge Wasser, die durch den Wasserhahn gelaufen ist, als sie im Bad war. Man könnte auch ihren älteren Bruder befragen usw. Auch diese Messwerte könnten ihre Probleme haben, geben uns aber zunehmend mehr Sicherheit für das Für und Wider der Hypthese.
Ein weiterer Punkt: wir können uns nie 100% sicher sein. Wenn ihre Mutte Jule z.B. um 18:00 daran erinnert hat Zähne zu putzen und Jule das sofort gemacht hat, der Tag warm war und im Bad die Heizung voll aufgedreht, weil es nachts noch kalt gewesen war, dann ist es nicht ausgeschlossen, dass die Zahnbürste 2 Stunden später schon wieder außen trocken ist und die Mutter, die die Zahnbürste nur äußerlich kontrolliert hat nun zu der Schlussfolgerung gekommen ist, die Zahnbürste wäre trocken.
Die Resultate solcher Untesuchungen sind immer nur mit einer bestimmten Wahrscheinlichkeit zutreffend oder unzutreffend.
Akzeptable Irrtumswahrscheinlichkeit
Häufig fordern Experimente oder Untersuchung ein sog. Signifikanzniveau. Oft liegt das bei 5%. In Formeln sagt man: p < 0.05 muss erfüllt sein. p ist der sog. Wahrscheinlichkeitswert. Und wir akzeptieren Untersuchungen dann, wenn Fehler in weniger als einem von 20 Fallen auftreten – bzw. in weniger als 5% der Fälle. Daher spricht man von einem 5%-Signifikanzniveau.
Beispiel: Wirkt das Medikament?
Betrachten wir z.B. die Wirksamkeit eines Medikaments. Ein Signifikanzniveau von 5% heißt nun, dass sofern wir sehen, dass ein Medikament statistisch signifikant wirksam ist, die Wahrscheinlichkeit, dafür, dass das reiner Zufall ist bei 5% liegt.
Zwar wird ein Wert von 5% oft verwendet, ist aber willkürlich. Gerade bei Medikamententest möchten wir vielleicht lieber ein Signifikanzniveau von 1% oder sogar 0,1%. Wir wollen also, dass die Irrtumswahrscheinlichkeit für die Wirksamkeit des Medikaments geringer ist.
Ergibt ein Signifikanztest beim Vergleich von zwei Gruppen von Patienten – eine mit und eine ohne Medikament – eine Heilungsdifferenz von 10% zugunsten der Gruppe mit Medikament und ergibt sich ferner dafür ein p-Wert von 0,0005, dann bedeutet das: die Wahrscheinlichkeit dafür, dass die Gruppe mit Medikament 10% schneller geheilt ist, ist mit einer Wahrscheinlichkeit von 0.05% auf den Zufall zurückzuführen. Also sehr unwahrscheinlich zufällig und daher sehr wahrscheinlich auf das Medikament zurückzuführen!
Wobei natürlich auch für diese Untersuchung ähnlich wie für die Betrachtung von Jule beim Zähneputzen gilt: auch, wenn die Untersuchung sehr für das Medikament spricht, kann es immer noch sein, dass wir nicht richtig oder nicht genug messen. Es könnte z.B. sein, dass die Gruppe mit Medikament im Mittel 20 Jahre jünger war, als die Gruppe ohne Medikament oder die Gruppe mit Medikament könnte sich jeden Tag Blaubeeren reinhauen, die entweder unabhängig vom und gemeinsam mit dem Medikament die Heilung positiv beeinfluss haben könnte. Daher ist es wichtig wie wir die Patienten für Studien oder allgemeiner die Attribute für unsere Untersuchung auswählen und zudem die Zusammenhänge zwischen den Attributen und dem Ergebnis untersuchen. Für Experimente, deren Ergebnis möglichst zweifelsfrei auf die Maßnahme (hier: das Medikament) zurückgeführt werden kann, müssen wir die Auswahl der Stichproble (hier: der Patienten) randomisieren, also zufällig gestalten und zusätzlich für wichtige Attribute kontrollieren: z.B. Alter, Ernährungsgewohnheiten, andere Erkrankungen, bestimmte Genausprägungen usw., wovon wir wissen, dass es die Untersuchungsergebnisse verfälschen könnte.
Im nächsten Artikel möchte ich zeigen wie man für einen konrekten Fall einen p-Wert berechnen kann.